Descrizione collettori solari a concentrazione 4 di 6
Ultimo aggiornamento Mercoledì 21 Marzo 2012 16:35 Scritto da Administrator Sabato 17 Marzo 2012 17:57
|
F |
Considerando la distribuzione del flusso di energia in funzione della posizione sulla superficie focale di un collettore cilindrico, come mostrato in figura , si ha che l’area totale della curva rappresenta l’energia totale riflessa sul piano focale. Se il ricevitore occupa tale zona solo fra il punto A ed il punto B, esso intercetterà l’energia rappresentata dalla zona tratteggiata.
Il fattore di intercettazione assume l’espressione:

Dove w è la distanza dal centro della zona focale.
Le prestazioni ottimali di un sistema si ottengono normalmente con un fattore di intercettazione minore di uno. In generale le dimensioni ottimali del ricevitore corrispondono alla massima energia utile raccolta e si calcolano minimizzando la somma delle perdite termiche ed ottiche; un ricevitore grande comporta elevate perdite termiche e basse perdite ottiche, mentre a un ricevitore piccolo corrispondono perdite termiche minori ma più elevate perdite ottiche a causa di un più basso coefficiente S.
Nel computo del fattore S entrano essenzialmente le perdite di energia per i seguenti motivi:
-
Errori ed irregolarità locali della superficie del riflettore sotto forma, da una parte, di microirregolarità di dimensioni paragonabili alla lunghezza d’onda della radiazione (presenza di riflessione diffusa oltre alla speculare), e dall’altra, sotto forma di piani infinitesimi locali con normale non coincidente con quella attesa teoricamente (presenza di riflessione speculare fuori bersaglio).
-
Errori macroscopici di forma e quindi distorsione dell’immagine.
-
Errori di posizionamento del riflettore rispetto al ricevitore
-
Errori di orientamento e di inseguimento solare del riflettore
La dispersione conseguente agli errori di cui al punto 1 si valutano attraverso un angolo eff di maggiore apertura del fascio teorico perfettamente collimato. Tale angolo, che porta il fascio ad avere una apertura maggiore del teorico (2 x 0,27°) aumenta le dimensioni dell’immagine in maniera proporzionale al raggio dello specchio ed alla distanza focale.
La presenza degli errori dovuti a diffusività locale e difformità dalla retta normale ideale, uniformemente distribuiti su tutta la superficie dello specchio, sono da ritenersi di natura puramente casuale e modellabili statisticamente con una distribuzione gaussuana dell’errore = eff - teor inteso come differenza fra l’angolo di riflessione reale e l’angolo teorico (2 x 0,27°).
La densità di probabilità in funzione dell’errore , è pertanto:

dove è la deviazione standard, indicatrice della bontà dello specchio, avendosi normalmente:
fino a 0,2 mrad (0,0115°) per superfici specchianti ottime
oltre 0,2 mrad e fino anche 8 mrad (0,45°) per superfici di media o cattiva qualità
Gli errori più significativi sono comunque legati ad errori macroscopici di forma e di posizionamento reciproco riflettore/ricevitore. Se si suppone che anche questi ultimi errori siano casuali, ipotizzando una distribuzione normale di Gauss sul piano focale, della radiazione incidente, si trova che il fattore S (omnicomprensivo di tutti gli errori sopra elencati) è proporzionale al rapporto r/R fra la distanza del punto generico del ricevitore dall’asse focale e la grandezza R intesa come distanza fra punto del riflettore e fuoco, cioè indicatrice dell’ampiezza della parabola.
In formula:

h è il coefficiente di distribuzione normale del flusso sul piano focale.
Il fattore S tende ad 1 per dimensioni notevoli del ricevitore , r, oppure per parabole di piccola apertura R.
I valori normalmente ammessi per l’errore dell’angolo di riflessione, per i concentratori parabolici, non superano 0,1 – 0,2° portando complessivamente il fattore S ad essere prossimo a 0,95 – 0,97 compresi anche gli effetti legati all’ultima delle quattro cause analizzate: errori di orientamento ed inseguimento solare.
TRASMITTANZA DELLA COPERTURA DEL RICEVITORE 7
La trasmittanza dell’eventuale rivestimento in vetro del ricevitore, se presente, riduce ulteriormente l’energia disponibile.
I parametri in gioco sono:
-
n indice di rifrazione 8
-
K fattore di estinzione
Ambedue questi fattori sono, per ogni materiale trasparente, funzione della lunghezza d’onda dell’energia incidente.
Trascurando per il momento la variabilità dei citati parametri ottici con la lunghezza d’onda, dalla relazione di Fresnel 9 che descrive la riflessione di una radiazione non polarizzata quando essa passa da un mezzo con indice di rifrazione relativa n all’aria (od al vuoto), e dalla legge di Snell che lega gli angoli di incidenza e rifrazione, per il materiale trasparente di rivestimento del ricevitore si ha un coefficiente di riflettanza dato dalla formula:
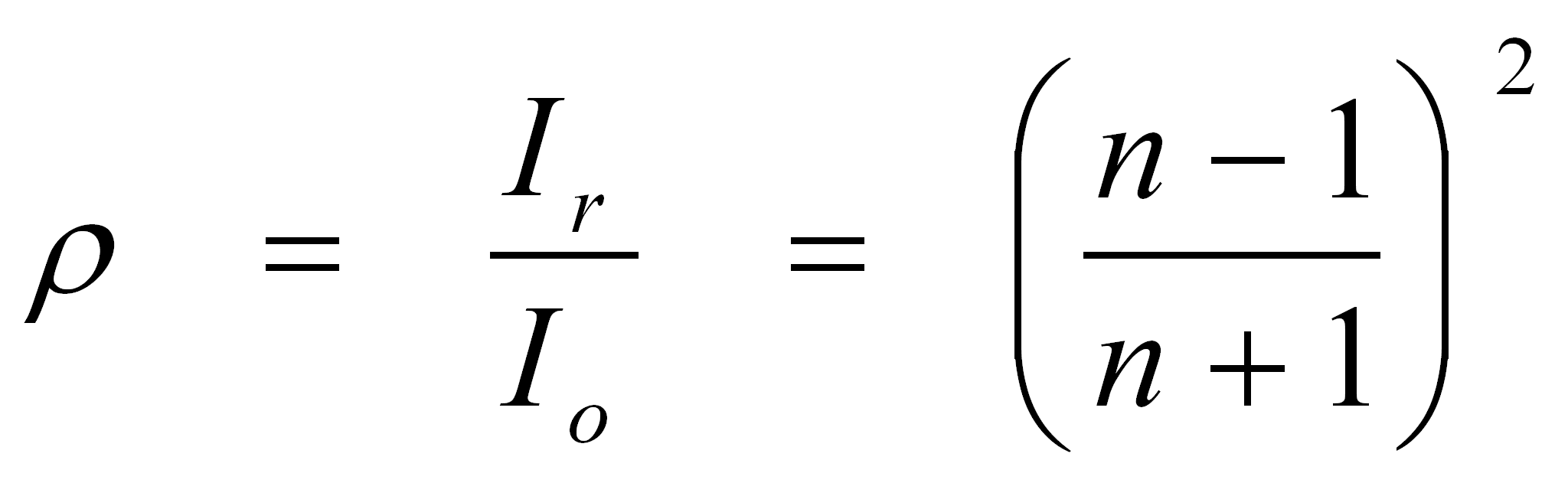
Il coefficiente di riflettanza , per ogni interfaccia di separazione vetro/aria o vetro/vuoto, rappresenta la quota di energia riflessa dalla superficie. Considerando le due interfacce della copertura, e tralasciando per il momento i fenomeni di assorbimento, la trasmittanza (parziale, considerando le sole perdite per riflessioni interne ed esterne) è:
![]()

Se si considera infine l’assorbimento dell’energia nell’attraversamento dello spessore di vetro della copertura, dalla legge di Bouger si ha:

dove K è il coefficiente di estinzione (m-1) ed L è la lunghezza del percorso (m).
Per tener conto di entrambi i fenomeni (riflessioni multiple ed assorbimento) una serie di formule valevoli nel caso di KL piccolo ( a prossimo ad uno) sono semplicemente le seguenti:
Trasmittanza totale = a r
Riflettanza totale R = a (1- r )
Assorbimento: = 1 - a
Le equazioni precedenti sono una accettabile semplificazione delle equazioni rigorose (dette di Stokes) che da considerazioni matematiche restituiscono i tre parametri , R, ed sia per la componente parallela che per quella normale di una radiazione non polarizzata incidente su una lastra di vetro, caratterizzata da spessore L, estinzione K, indice di rifrazione n
Il tipo di vetro10 normalmente usato per il rivestimento dei ricevitori è un vetro al borosilicato commercialmente noto con il nome di PYREX (o DURAN od ancora KIMAX). Le sue caratteristiche sono:
SiO2 81%
Al2O3 2 – 2,5%
Na2O 4 – 4,5%
B2O3 12 – 13%
Coefficiente di dilatazione: 33 10-7 /°C
Temperatura di rammollimento: 820 °C
Temperatura di esercizio max: 450 – 500 °C
Calore specifico (0°C): 0,8 KJ/Kg °C
Conduc. termica (0°C): 1,17 KJ/m s °C
Indice di rifrazione (media da 0,4 a 2,3 ): 1,511
Indice di riflessione (media da 0,4 a 2,3 ): 0,0414
Indice di trasmittanza (media da 0,4 a 2,3 ): 0,9973 (con spessore 3 mm)
Coefficiente di estinzione (media da 0,4 a 2,3 ): < 10 m-1
(il coef. di estinzione di un normale vetro chiaro è > di 30 m-1)
Gli spessori impiegati per applicazioni su collettori parabolici lineari si aggirano su 3 millimetri. Le superfici sono generalmente trattate con opportuni strati antiriflesso che, nel campo dello spettro solare, riducono la riflessione dal valore nominale del citato 4% a valori trascurabilmente inferiori all’ 1%.
Dato che la riflessione aumenta all’aumentare del rapporto n2/n1 dei due indici assoluti di rifrazione dei materiali a contatto, uno strato antiriflettente (AR) dovrà avere un indice assoluto di rifrazione nAR tale da poter minimizzare contemporaneamente il rapporto nAR/n1 ed il rapporto n2/nAR. Con un solo strato antiriflettente si ha il valore ottimale di ![]() essendo il materiale 1 aria (n1 = 1) ed il materiale 2 vetro11.
essendo il materiale 1 aria (n1 = 1) ed il materiale 2 vetro11.
Nel calcolo delle caratteristiche ottiche bisogna tener conto che esse, nella realtà dipendono dalla lunghezza d’onda della radiazione, per cui, per esempio, il coefficiente di trasmittanza della radiazione diretta su un materiale trasparente è più precisamente definibile dalla:

Dove G() è l’irraggiamento monocromatico incidente e () il coefficiente di trasmissione monocromatico.
Nell’andamento di () influisce notevolmente la variazione dell’indice di rifrazione (e quindi di riflessione) del vetro in funzione della lunghezza d’onda, mentre è trascurabile la variazione del coefficiente di estinzione (K) che, per esempio nel caso di un vetro PYREX, nel campo delle lunghezze d’onda 0,3 -.2,7 , si mantiene costantemente < 10 m-1.
Nelle figure seguenti sono riportati alcuni dati relativi al vetro PYREX “BSC517642B” commercializato dalla ditta Pilkington12. Essi sono relativi al campo dello spettro solare e, per la trasmittanza a (quota conseguente alla sola estinzione) è stato assunto uno spessore di 3 mm e nessun trattamento antiriflesso
.

Fig. A4.19 – Indice di rifrazione vetro PYREX

Fig. A4.20– Indice di riflessione vetro PYREX

Fig. A4.21 – Trasmittanza vetro PYREX
Una ulteriore limitazione teorica alle considerazioni sopra riportate deriva dal fatto che le equazioni fin qui richiamate (per la determinazione della riflettanza e della trasmittanza) sono rigorosamente valide solo per un angolo nullo di incidenza della radiazione rispetto alla superficie del vetro.
Per fortuna nella maggior parte dei casi pratici è superfluo ricorrere alla originaria formulazione delle equazioni di Fresnel e di Stokes (che tengono conto anche dell’angolo di incidenza), dato che l’errore introdotto dalle equazioni semplificate è minore dell’1% per angoli fino a 60°, e quasi inesistente per angoli di fino a 20 – 30°. Un buon progetto di un collettore solare d’altronde rispetterà questi valori limite di angolo di incidenza anche e soprattutto per le più pesanti penalizzazioni legate al decremento di altri importanti parametri (assorbanza/emittenza del ricevitore).
ASSORBANZA ED EMITTENZA
Ai fini del bilancio termico globale del collettore hanno ben maggiore importanza le proprietà radiative del materiale costituente il vero e proprio ricevitore. Esse dipendono, per ogni materiale, dalla lunghezza d’onda, dalla direzione di incidenza, dalla temperatura della superficie e dal suo stato chimico fisico.
E’ indubbiamente conveniente usare nei collettori solari dei materiali, o dei rivestimenti aventi un elevato coefficiente di assorbanza () nel campo delle lunghezze d’onda dello spettro solare (da 0,2 a 2,5 ) ed un basso coefficiente di emittanza () per le lunghezze d’onda maggiori, tipiche della radiazione infrarossa ed oltre.
Infatti una radiazione solare diretta al suolo standard di una tipica situazione (con DNI totale di 900 W/m2) ha una distribuzione spettrale continua come quella riportata in figura A4.22 (I valori sono stati ricavati dai valori di 20 fasce di lunghezza d’onda che presentino fra di loro lo stesso contenuto energetico).
Sovrapponendo lo spettro solare a quello del corpo nero per varie temperature di emissione (temperature di funzionamento a regime del ricevitore solare) si ha per esempio la situazione della figura seguente (A4.23) dalla quale si evince che esiste una zona di separazione (in termini di lunghezza d’onda) fra i due tipi di energia radiante.
Questa lunghezza d’onda di separazione, variabile con la temperatura del collettore (comunque intorno a 2 – 3 ) dovrebbe essere il punto di discontinuità fra un comportamento ideale da corpo nero (=1, assorbitore perfetto) ed un comportamento teorico da specchio ( = 0 nessuna perdita radiativa).

Fig. A4.22 – Spettro solare su superficie terrestre, tipico

Fig. A4.23 – Spettro solare e di emissione del corpo nero
Segue pagina 5 di 6











 ig. A4.18 – Energia su ricevitore
ig. A4.18 – Energia su ricevitore