Descrizione collettori solari a concentrazione. 1 di 6

Última actualización en Miércoles, 21 de Marzo de 2012 16:23 Escrito por Administrator Sábado, 17 de Marzo de 2012 16:27

 

Collettori a concentrazione per l’impiego dell’energia termica solare

(Per gentile concessione di Carlo Zamparelli)

 

Carlo ZAMPARELLI  

Aprile 2006

 

 

Collettori a concentrazione per l’impiego

 dell’energia termica solare

 

 INDICE

 

 

1. INTRODUZIONE  

2. I COLLETTORI SOLARI A CONCENTRAZIONE 

3. BILANCIO TERMICO REALE  

4. CARATTERISTICHE TERMO – OTTICHE  

5. STATO DELL’ARTE E PROSPETTIVE FUTURE  

6. CONCLUSIONI  

7. BIBLIOGRAFIA  

 

 

INTRODUZIONE

  

 

 

 

 

 

 

 

Concentratore parabolico lineare Ricevitore Tubolare	Concentratore parabolico tridimensionale Ricevitore piano
Concentratore multiplo a parabolidi Ricevitore Piano	Concentratore Fresnel a rifrazione Ricevitore Piano
Concentratore Fresnel lineare Ricevitore Tubolare	Concentratore ad ottica non-imaging Ricevitore piano
Concentratore ad eliostati piani Ricevitore piano od a cavità	Concentratore doppio (eliostati + parabolide) Ricevitore a cavità per fornace solare

 

 

I COLLETTORI SOLARI A CONCENTRAZIONE

 

 

Il collettore solare è il componente principale dei dispositivi che trasformano l’energia solare radiante che giunge al suolo in energia termica utile. Il collettore solare differisce per molti aspetti dagli scambiatori di calore convenzionali. Questi ultimi di solito realizzano uno scambio termico da fluido a fluido con elevata efficienza di trasferimento, mentre la radiazione termica è un fenomeno secondario. Nel collettore solare il trasferimento di energia avviene, esclusivamente per irraggiamento, tra una sorgente di energia radiante ed un corpo ricevitore.

Senza concentrazione ottica il flusso di radiazione solare incidente è al più attorno a 900 W/m² ed è variabile con i parametri geografici, stagionali ed orari; i collettori piani, per produzione di acqua calda o per conversione fotovoltaica, senza concentrazione, hanno il vantaggio di utilizzare sia la radiazione solare diretta che diffusa; presentano scarsa necessità di orientamento e sono più semplici ed economici dei collettori a concentrazione.

 

I collettori a concentrazione (a focheggiamento) hanno normalmente dei riflettori concavi o dei campi di specchi che concentrano la radiazione incidente sull’area totale del riflettore su un ricevitore di area minore e pertanto investito da un flusso di energia maggiore. Con i collettori a focheggiamento si raggiungono altissime temperature, anche fino a 3000 °C come per esempio nelle fornaci solari..

 

Con il termine “collettore”, nei sistemi a concentrazione, si intenderà il sistema completo, comprendente il concentratore ed il dispositivo ricevitore di raccolta. Il concentratore, o sistema ottico, è la parte del collettore che dirige la radiazione sul ricevitore; in questa analisi considereremo solamente i sistemi ottici basati sulla riflessione, cioè gli specchi.

Il ricevitore è quell’elemento del sistema dove viene assorbita la radiazione e convertita in qualche altra forma di energia utile.

L’assorbitore sarà una parte, assieme ad eventuali sistemi di copertura ed isolamento, del ricevitore e consiste spesso in un suo strato superficiale esterno direttamente investito dalla radiazione.

Per impieghi in impianti industriali di potenza, come centrali elettriche solari o reattori solari chimici, sono giunte a maturità configurazioni di specchi basate su forme paraboliche, sia sviluppate longitudinalmente come risultato della traslazione di una parabola (geometricamente un cilindro con sezione trasversale a forma di parabola, con focheggiamento su una linea), sia come solido di rivoluzione nei paraboloidi a fuoco puntiforme.

 

L’aumento di flusso termico ottenuto è messo in luce dal principale parametro dei collettori di cui stiamo trattando: il rapporto di concentrazione C.

 

C = A / A_r

 

A è l’area di apertura del concentratore, cioè dello specchio, misurata sul piano normale all’asse della parabola o del paraboloide; essa rende conto dell’energia solare ricevuta.

A_r è l’area del ricevitore che intercetti il 100% dei raggi riflessi ed è da tenere in conto per il calcolo delle perdite (fra le principali il reirraggiamento dovuto alla temperatura di esercizio del ricevitore).

 

Nel caso di un collettore a paraboloide (chiamato anche “solar dish”) l’area A sarà l’area del cerchio massimo di troncamento del solido di rivoluzione secondo un piano normale all’asse, ed A_r rappresenta la superficie del ricevitore ideale captante al meglio tutti i raggi solari riflessi. Il ricevitore potrà essere un disco piano, una sfera, od un qualunque altro solido geometrico.

Se il collettore è esteso solo in due dimensioni (collettori cilindrici parabolici), avendosi la stessa lunghezza per lo specchio e per il ricevitore, le due aree sono sostituite da una parte dall’apertura della parabola alla sua sommità, e dall’altra dalla larghezza del corpo ricevitore, o dalla circonferenza dell’eventuale tubo in posizione focale.

 

Dalla precedente definizione si arguisce come lo stesso concetto di rapporto di concentrazione porti a valori notevolmente diversi fra il caso tridimensionale del paraboloide e bidimensionale del cilindro parabolico: nel primo caso, a parità di parabola generatrice, si ha un rapporto di concentrazione che segue la legge del quadrato del rapporto delle lunghezze.

 

A rigore dal computo della superficie A andrebbe detratta la proiezione di A_r che ombreggiando il concentratore riduce la radiazione solare raccolta. In effetti è lecito, visti i rapporti di dimensioni in gioco, trascurare questo effetto di ombreggiamneto, anche perché la sottostima dell’energia solare raccolta (e trasmessa al ricevitore) è compensata dal fatto che lo stesso ricevitore, almeno in parte, è normalmente esposto alla radiazione diretta solare intercettata direttamente prima di essere concentrata dagli specchi.

 

L’importanza del rapporto di concentrazione (che si ripercuoterà sui valori delle temperature di esercizio) deriva dal fatto che il sole, anche se visto alla distanza sole-terra, non può essere schematizzato come un punto geometrico. Se così fosse i suoi raggi giungendo sulla terra in modo pressocchè parallelo fra di loro, secondo le leggi dell’ottica geometrica potrebbero essere focalizzati in un punto piccolo a piacere, con la conseguenza di potere raggiungere, almeno teoricamente, rapporti di concentrazione infiniti.

Con le distanze e le dimensioni di cui stiamo trattando si ha la configurazione schematizzata in fig.A4.1

 

Fig. A4.1 – Angoli di visuale del sole

 

Pur potendo trascurare l’angolo  fra i raggi provenienti da uno stesso punto del disco solare (errore inferiori a 10 ^–9), non è certamente trascurabile, per i nostri scopi l’angolo sotto al quale è visto sulla terra il diametro solare: esso è di circa mezzo grado variando leggermente in funzione della distanza sole/terra, dell’altezza solare sull’orizzonte e quindi della rifrazione atmosferica. Nelle considerazioni seguenti verrà assunto costante ed uguale a 0,534°.

 

Conseguenza di quanto sopra è che assieme ai raggi solari centrali, che attraverso un opportuno puntamento dello specchio arrivano con direzione assiale, saranno presenti raggi con deviazione + e -  ( = 0,534 / 2 = 0,267°) colpenti lo stesso punto della superficie dello specchio ed assoggettati separatamente alle leggi dell’ottica geometrica.

 

 

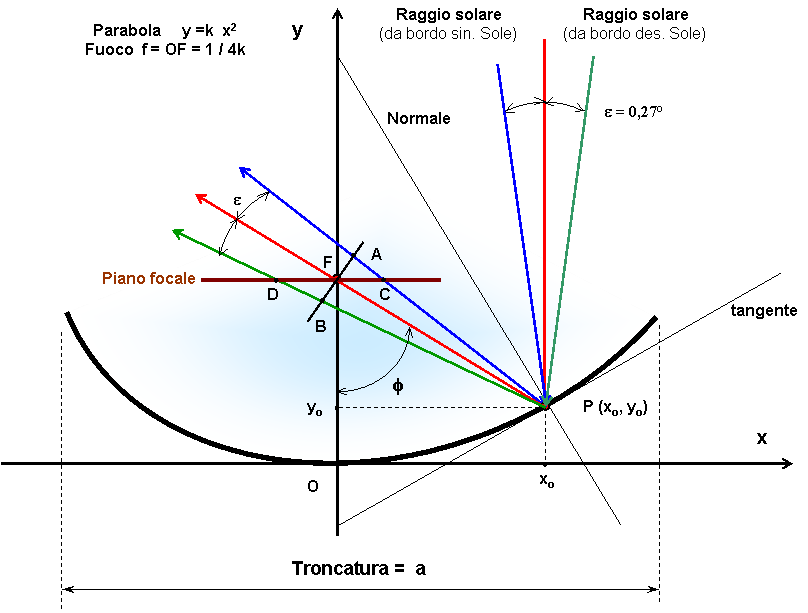
Fig. A4.2 – Formazione della macchia solare su piano focale

 

Assegnata una parabola generica di vertice O ed equazione y = k x² (con fuoco f = 1/4k), le equazioni dei tre raggi riflessi dal generico punto P dello specchio, di coordinate (x₀, y₀), saranno, in funzione dell’ascissa x₀ del punto di impatto:

 

Raggio centrato y = k x₀² + x₀ / tg 2_n - x /tg 2_n

Raggio da bordo destro sole y = k x₀² + x₀ / tg (2_n + ) - x /tg (2_n + )

Raggio da bordo sinistro sole y = k x₀² + x₀ / tg (2_n - ) - x /tg (2_n - )

 

Dove _n è l’angolo della normale alla parabola nel suo punto P (x₀, y₀):

_n = arctg (- 1 / 2kx₀)

Le precedenti equazioni per x=0 restituiscono la distanza fra il vertice e l’intersezione con l’asse della parabola del raggio riflesso dal punto (x₀, y₀); per y = fuoco = 1/4k restituiscono la deviazione in orizzontale, sul piano focale, di detto raggio rispetto al fuoco ottico.

I principali parametri della parabola, per usi ottici, sono la sua lunghezza focale (f) responsabile della grandezza dell’immagine focalizzata ed il valore di troncatura (a) responsabile della quantità di energia che incide sul dispositivo e che sarà concentrata in un’area di dimensioni minori. La brillantezza dell’immagine (il fattore di concentrazione dell’energia) sarà quindi proporzionale al rapporto dei due parametri.

E’ uso comune trattare i problemi geometrici ed energetici di questi tipi di collettori in funzione del parametro adimensionale f/a.

Nelle considerazioni seguenti, relative alla teoria geometrica di un concentratore parabolico, considereremo, per il momento, la variabile indipendente f/a in tutto il suo dominio di esistenza a prescindere dalle limitazioni pratiche e tecnologiche che impediscono di fatto di poter disporre di dispositivi ottici per immagini con f/a molto piccolo; tale limite è attorno al valore dell’unità.

 

L’angolo di troncatola  (come definito nella figura precedente) in funzione dell’indice f/a, risulta:

Nella seguente figura riportiamo in grafico la suddetta relazione geometrica.

 

 

La dimensione dell’impronta solare sul piano focale, dimensione della zona che raccolga al meglio il 100% dei raggi solari provenienti da tutta l’estensione della parabola, sarà diversa a seconda della sua geometria, piana, cilindrica, sferica, etc.

 

In dettaglio sul piano focale si avrà la seguente configurazione:

 

 

 

 

La dimensione dell’immagine per un concentratore lineare e ricevitore piano sarà:

 

ed il relativo rapporto di concentrazione (con pari lunghezza longitudinale del concentratore e del ricevitore):

 

L’andamento teorico del rapporto di concentrazione, in questo caso, sia in funzione dell’angolo di troncatura che in funzione del parametro f/a è pertanto quello evidenziato nei due grafici seguenti. Da considerazioni analitiche si ricava il massimo di c = f() che vale c _max = 1/(2 tan 0,267) - 1/4 = 107 per  = 45°

 

Nel caso che il ricevitore sia di forma tubolare cilindrico i raggi solari invilupperanno una circonferenza di diametro AB come schematicamente indicato nel disegno …..Il primo relativo ad un concentratore con angolo di troncatura minore di 90° (cioè con fuoco esterno alla superficie di troncatura) ed il secondo con angolo maggiore (cioè parabola molto avvolgente il suo fuoco).

 

 

Con un concentratore lineare e ricevitore cilindrico, della stessa lunghezza, si ha:

 

Che presenta il suo valore massimo per  = 90° ¹

 

 

 

 

 

 

La trattazione del concentratore tridimensionale (paraboloide), sia per ricevitore piano che anch’esso tridimensionale (in questo caso ipotizzato sferico) è simile alla precedente, dove ora l’area del concentratore è A =  a²/4 e l’area del ricevitore è rispettivamente nei due casi, A_r =  D²/4 (ric.piano) e A_r =  D² (ric. sferico)

 

Il valore massimo del rapporto di concentrazione risulta in ambedue i casi

C _max = 11500 per angoli di troncatura, rispettivamente di 45° e 90°

 

 

 

 

 

 

Il valore minimo della macchia solare, a parità di forma geometrica della parabola, cioè a parità di valore f del suo fuoco, si ha per x₀ = 0 (raggio solare incidente nel vertice) ed il suo valore massimo, che è quello di nostro interesse, per x₀ coincidente con la semiampiezza della parabola.

Per esempio nel caso di una parabola commerciale, normalmente utilizzata negli impianti elettrici solari a collettori parabolici lineari² ( y = 0,138 x²) si ha:

 

CD _min = 0,01677 metri e CD _max = 0,0708 metri con semiampiezza x₀ = 2,5 metri

 

 

Il loro andamento dimostra l’impossibilità di andare oltre il valore di circa 100, e la presenza per ogni tipo di parabola di una sua ampiezza ottimale.

 

 

Nella pratica realizzativa di questi collettori bidimensionali il ricevitore è di norma una tubazione con il proprio asse lungo la linea focale del cilindro parabolico. In tal caso, anche in presenza di parabole con profondità minore del loro fuoco, i raggi estremi inviluppano una superficie circolare, potendo individuare una circonferenza che sicuramente intercetti tutti i raggi riflessi con deviazione +/-  da qualunque punto della parabola.

 

I valori di concentrazione massima ricavati nei casi precedenti sulla base di semplici considerazioni geometriche, sono notevolmente minori dei valori massimi teoricamente raggiungibili in base a considerazioni di termodinamica cui accenneremo poco oltre. Infatti, pur avendo considerato dei concentratori (specchi) perfetti in quanto ad errori geometrici di riflessività la macchia solare presenta una densità di energia disuniforme lungo la direzione normale all’asse ottico: per zone vicine all’asse si hanno aree elementari più piccole a pari corrispondente area del concentratore per cui è ipotizzabile di poter teoricamente disporre di un collettore che, con densità di flusso sul ricevitore costante ed uguale al suo valore massimo, presenti fattori di concentrazione superiori. Il fenomeno è ulteriormente esaltato dalla non uniformità della radiazione da parte del sole fra suo centro e bordi, con maggiori valori in corrispondenza dei raggi centrali che puntano ovviamente sul fuoco geometrico del concentratore.

 

Per esempio nel caso di un concentratore parabolico lineare e ricevitore piano il valore di concentrazione massimo prima trovato (c = 107 per  = 45°) non tiene conto che in realtà il suo valore locale puntuale è di oltre 200 nelle zone centrali del ricevitore, per decadere rapidamente a zero entro al massimo una distanza di circa 10 millesimi del valore della lunghezza focale.

 

 

 

 

In definitiva essendo ogni parabola caratterizzata da un valore del fuoco (f), il parametro di qualità ai fini della concentrazione energetica solare risulta semplicemente proporzionale ad f/a, essendo l’ampiezza a determinante per la quantità di energia coinvolta ed f determinante per le dimensioni dell’immagine solare.

 

Come esempio analizzando un ipotetico specchio tridimensionale a forma di paraboloide, di notevole distanza focale, per esempio 100 metri e con ricevitore ipotizzato su un piano normale all’asse della parabola, riprendendo il grafico di fig. A4.10. riportiamo la relazione che lega il rapporto di concentrazione alla semiampiezza dello specchio in corrispondenza del suo piano di troncatura. Dal grafico seguente è evidente che, assegnato un certo fuoco, per ottenere un determinato rapporto di concentrazione (che come vedremo è a sua volta imposto dal bilancio termico del processo) si beve scegliere una ben determinata dimensione geometrica.

 

Fig. A4.12 - Relazione fra C ed x_o = a/2 per paraboloide e ricevitore piano

 

 

Gli alti valori raggiungibili da parte del rapporto di concentrazione rendono ragione della necessità, per questa famiglia di collettori, di un inseguimento continuo dei raggi solari e della influenza che fattori geometrici, meccanici, etc possono avere sul rendimento termico globale.

 

 

LIMITI TERMODINAMICI DEL RAPPORTO DI CONCENTRAZIONE

 

Il fatto che, come si evince da tutti i casi trattati, esista un valore massimo conseguibile da parte del concentratore, numericamente indipendente dal tipo di parabola, è confermato teoricamente anche da considerazioni basate sul secondo principio della termodinamica che, a prescindere dalla forma e dal tipo di concentratore (parabolico, piano, a riflessione, a rifrazione, etc..), pongono i vincoli teorici sotto riportati.

 

Consideriamo un concentratore tridimensionale a disco di area di apertura A ed un ricevitore di area A_r ad una distanza R dal centro del sole il cui raggio sia r. Ipotizzando sia il sole che il ricevitore siano corpi neri perfetti alle rispettive temperature T_s e T_r la radiazione emessa dal sole è:

Q_s = (4r²) T_s⁴

 

Di cui la frazione F_sr = A / 4R² è intercettata dal collettore ed inviata al ricevitore. Pertanto l’energia emessa dal sole e ricevuta dal ricevitore è:

Q_sr = A (4r² / 4R² ) T_s⁴ = A (r²/R²) T_s⁴

 

Similmente l’energia irradiata dal ricevitore verso il sole è:

Q_rs = Ar F_rs T_r⁴

 

Dove F_rs è il fattore di vista dal ricevitore al sole, che tiene conto della frazione di energia emessa dal ricevitore e che raggiunge il sole.

Coerentemente con la seconda legge della termodinamica non vi può essere scambio di energia fra due corpi alla stessa temperatura; per cui se T_s = T_r si deve necessariamente avere Q_sr = Q_rs, ovvero:

 

A / A_r = R²/r² F_rs

 

Poiché F_rs è al massimo uguale ad 1, il massimo teorico del rapporto di concentrazione A/A_r per il caso tridimensionale è:

C _{max 3} = R² / r² = 1/sen² 

E per il caso bidimensionale, sostituendo al rapporto delle aree il rapporto delle lunghezze:

C _{max 2} = R / r = 1/sen 

 

Con il valore adottato di  = 0,267° si ottiene il limite teorico termodinamico dei rapporti di concentrazione, rispettivamente per il caso tridimensionale e bidimensionale:

 

C _{max 3} = 45.000

C _{max 2} = 212

 

 

LIMITI OTTICI DEL RAPPORTO DI CONCENTRAZIONE

 

Una trattazione sui limiti del fattore C può essere condotta anche con strumenti più attinenti al caso in esame, cioè basandosi sulle leggi dell’ottica che fra l’altro, con i relaltivi risultati, faranno intravedere l’opportunità di ricorrere a volte, per la concentrazione dell’energia solare, alla teoria dell’ottica “non-imaging” ed all’utilizzo di dispositivi che abbandonino il requisito di rimpicciolire l’immagine che si presenta sul piano di ingresso del concentratore.

Generalizzando il concentratore come una scatola dotata di apertura di ingresso di superficie A e diametro a (superficie di raccolta dell’energia) ed un ricevitore di superficie A’ e diametro a’, a distanza f fra di loro, sia  la semiampiezza dell’angolo massimo di divergenza di un raggio normale alla superficie A. Similmente indicheremo con ’ il corrispondente angolo di divergenza sulla superficie del ricevitore.

 

 

 

 

 

La teoria della formazione delle immagini dimostra la relazione di Abbe:

dove n ed n’ sono gli indici di rifrazione dei due mezzi, rispettivamente posti a monte della superficie A ed a valle di A’

In un concentratore tridimensionale quindi:

 

 

La precedente formula è valida a prescindere dal tipo e forma del concentratore,; è valida per concentratori a riflessione o a rifrazione, per concentratori di immagini o meno, simmettrici od asimmetrici.

Il valore massimo del fattore di concentrazione, cioè la più piccola superficie che, a parità di superficie di apertura A, è in grado di raccogliere tutti i raggi in ingresso, si ottiene quando i raggi sul ricevitore presentano un angolo di divergenza fino a 90°, fermo restando l’angolo di divergenza in ingresso ().

 

In corrispondenza dell’angolo ’ generico si ha inoltre la seguente relazione ottica generale:

f/a = 1 / 2 tg ’

Nei casi di nostro interesse, si riconferma il limite termodinamico tridimensionale (C _max = 45000) ponendo  = 0,267° (semiampiezza della dimensione apparente del sole) e n = n’ = 1 (sistemi in presenza di aria e/o vuoto).

Il corrispondente valore di f/a sarebbe in tale caso, matematicamente, nullo: conferma del fatto che siamo in presenza di un limite teorico raggiungibile al limite con superficie di ingresso infinita o focale del dispositivo nulla.

 

Il grafico seguente presenta l’andamento del fattore di concentrazione teorico (per n = n’ =1) e l’andamento dell’indice f/a che un simile dispositivo ottico di conseguenza dovrebbe avere, ambedue in funzione del massimo angolo di divergenza (’): dei raggi sul ricevitore.

 

Volendo restare nel campo dell’ottica per immagini è quasi impossibile realizzare dispositivi con f/a <1 per la presenza dei fenomeni di aberrazione che impedirebbero la corretta formazione delle immagini. Ne consegue, dal grafico precedente, che il limite effettivo del rapporto di concentrazione è di circa 10000; se inoltre si mettono in conto gli errori geometrici del collettore o del sistema di puntamento solare tali da far si che il raggio centrale del cono di divergenza (cono solidi di angolo 2 ) non sia telecentrico (parallelo all’asse ottico), la divergenza totale in ingresso e sul ricevitore aumenta limitando ancor più il valore di concentrazione conseguibile.

 

Nel campo dell’ottica “non-imaging”³ questi limiti non sono condizionanti rimanendo pienamente valido, anche in pratica, il limite di concentrazione posto dalla legge di Abbe; nelle realizzazioni pratiche si ottiene un aumento del fattore di concentrazione, rispetto ai sistemi ad immagine, di un fattore 4 od oltre, molto vicino quindi ai limiti teorici visti precedentemente.

In un sistema per immagini tutti i raggi in ingresso attraversano o si riflettono lo stesso numero di volte (nei casi semplici una sola volta) su ogni superficie del dispositivo e la lontananza dal limite teorico è data essenzialmente dai fenomeni di aberrazione; nei sistemi “non imaging”, invece, raggi diversi presentano varie volte, e differenti fra di loro, rifrazioni/riflessioni sulle superfici, e sono solo quei raggi che sfuggissero indietro a differenziare il sistema dal suo comportamento ideale.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 APPLICAZIONI TERMODINAMICHE

  Schematizziamo un collettore solare a concentrazione con un generico sistema di captazione dell’irraggiamento solare (di superficie A) che contemporaneamente provveda alla sua concentrazione, non importa per il momento se tramite rifrazione o riflessione.

Il ricevitore finale dell’energia solare abbia superficie A_R e si trovi, a regime ad una temperatura funzione del rapporto di concentrazione c = A / A_R.

 

Il flusso di energia in ingresso al sistema, W_S, è costituito dall’irraggiamento solare, corretto con tutta una serie di fattori funzione del reale assetto costruttivo del dispositivo. Infatti occorre:

 

• Tener conto della sola componente solare diretta, trattandosi di concentratori ottici;

• Utilizzare di questa componente diretta la sola componente normale al piano di captazione: essa sarà la cosiddetta DNI (Direct Normal Irradiation) per i sistemi ad inseguimento solare su due assi, e (DNI cos i) per quelli a singolo asse, dove i è l’angolo di incidenza fra il raggio solare e la normale alla superficie di raccolta del concentratore;

• Ridurre il flusso di energia in ingresso con fattori che tengano conto di errori di geometria e/o posizionamento (fattore “S” – Spillage), della riflettività reale degli eventuali specchi (), del coefficiente di trasmissione da parte di eventuali setti di vetro od altro materiale trasparente (), del potere di assorbimento della radiazione solare da parte del ricevitore che non si comporta come un ideale corpo nero (); tutti fattori minori dell’unità e funzione oltre che della composizione spettrale dell’energia, del suo angolo di incidenza sulle superfici interessate.

 

Per la seguente trattazione semplificata assumeremo W_S un dato del problema, ricavato da misure sperimentali e già al netto di tutte le correzioni sopra ricordate. W_S costituirà pertanto l’energia utile in ingresso al dispositivo. Per le simulazioni seguenti potremmo porre in prima approssimazione W_S = 900 W/m² e considerarlo come valore nominale (valore di picco, per i suoi ovvi legami con la data, l’ora e la localizzazione geografica) dell’input energetico del sistema.

I bilanci termici e le deduzioni che ne trarremo sono inoltre svolti nell’ipotesi di trascurare gli scambi termici convettivi e conduttivi fra il ricevitore e l’ambiente a temperatura costante T_a. Questa ipotesi, molto lontana dalla realtà per i sistemi a concentrazione unitaria, rappresenta invece una accettabile schematizzazione per i sistemi ad alta concentrazione, ad alta temperatura, spesso realizzati con accortezze tecniche atte a diminuire i due scambi termici trascurati: ricevitori sotto vuoto, cavità riceventi adiabatiche, etc..

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 Con le ipotesi precedenti, nel caso di concentrazione unitaria, la temperatura di regime (T₁) del ricevitore si ricava semplicemente dal bilancio:

 W_S =  (T₁)  T₁⁴ ( = 5,67 10 ^-8 W/m² K)

 

Temperatura T1 di regime del ricevitore con c =1 e W = 900 /m2				Caso extraatm. e corpo nero
Corpo nero  = 1	 = 0,9	 = 0,5	 = 0,1
355 K	364 K	422 K	631 K	394 K
82 °C	91 °C	149 °C	358 °C	121 °C

 

L’esperienza ci porta a considerare, in simili casi, temperature notevolmente inferiori alle suddette, non potendosi trascurare il fatto che il corpo ricevitore presenta spesso assorbanze solari molto minori di 1 (decurtando quindi notevolmente il supposto input di 900 W/m²), ed inoltre il fatto che in tale range di temperature le perdite convettive e conduttive giocano un ruolo fondamentale. Come riferimento si tenga presente che una lastra di alluminio al sole (assorbanza solare  = 0,3 ed emittenza a bassa temperatura  = 0,04) si assesta, con ordinarie condizioni ambientali, ad una temperatura non superiore ai 40 °C.

 

 

Tornando alla schematizzazione del fenomeno ideale la temperatura massima di un ricevitore solare con concentrazione unitaria sarà:

 

 

 

Dove  (T₁) è iterativamente calcolato per la temperatura di regime, e comunque quasi indipendente da essa, trattandosi di un campo di variazione molto ristretto.

 

Per le considerazioni seguenti sarà comodo scrivere questa temperatura come un multiplo della temperatura ambiente T₁ = k T_a

 

Nel caso di fattori di concentrazione maggiori dell’unità, il flusso di energia in ingresso al sistema sarà sempre uguale al precedente valore W_S =  (T₁)  T₁⁴

Per cui il nuovo bilancio assume la forma:

 

 (T₁)  T₁⁴ A = =  (T_C)  T_c⁴ A/c

 

Scrivendo la temperatura T_c come multiplo dell’ideale temperatura T₁ ricavata precedentemente si ha:

 

 (T₁) T₁⁴ = =  (T_C) (hT₁)⁴ 1/c

 

E quindi un innalzamento della temperatura di regime, rispetto alla concentrazione unitaria, secondo un fattore h:

 

 

La nuova temperatura di regime sarà:

 

⁴

 

 

Dove  (T_C) è iterativamente calcolato per la temperatura di regime (emissività nel campo dell’infrarosso).

 

 

 

Al solito riportiamo qualche valore della temperatura T_C con le consuete ipotesi di W = 900 W/m² ed assenza di perdite convettive/conduttive.

 

 

 

	Temperatura di regime TC del ricevitore solare (c > 1) [°C]
Fattore di concentrazione: c	 (TC) = 1	 (TC) = 0,5	 (TC) = 0,1
10	358	477	849
100	849	1062	1723
1000	1723	2100	3276
10000	3276	3948	6039

 

 

In tutte le considerazioni precedenti si è supposto nullo ogni altra asportazione di calore dalla superficie A_R ; in particolare si è immaginata l’assenza di qualsivoglia macchina termica che utilizzi parte dell’energia W_S.

In presenza di un utilizzo termodinamico dell’energia solare sarà W_S > W_R , la temperatura di regime di A_R (T_Cu : temperatura dell’energia utile per produrre lavoro) sarà minore della precedente Tc , e l’energia disponibile per la conversione termodinamica sarà W_S - W_R .

 

Chiamando h_u il nuovo fattore di aumento della temperatura del ricevitore, rispetto alla temperatura T₁ , il rendimento di concentrazione solare è:

 

 

 

Che ha il valore massimo per h_u =1 , ed il valore minimo (in particolare nullo) in corrispondenza del valore

 

(Da notare che il rapporto è molto prossimo all’unità, almeno nelle superfici metalliche ordinarie non impieganti rivestimenti selettivi).

 

 

 

 

 

 

 

 

Il rendimento termodinamico massimo di una ipotetica macchina termica funzionante fra la temperatura del ricevitore T_C = h_u T₁ e quella dell’ambiente T_a = T₁ / k

è dato da:

 

 

 

Il rendimento totale del dispositivo è allora:

 

 

Per visualizzarne l’andamento, cogliendone il significato, in funzione di h_u, cioè in definitiva in funzione della temperatura di esercizio del ricevitore solare, sarà bene, per il momento semplificare il problema ponendo = 1 ed assumendo k = 1.

 

La seconda ipotesi vuol dire ipotizzare la temperatura ambiente in pratica coincidente con quella del ricevitore senza concentrazione, mentre la prima significa trascurare le variazioni dell’emissività in tutto il campo dell’infrarosso (da una lunghezza d’onda di 2 micron in poi).

In realtà invece, i metalli, specie se ossidati, presentano una curva di emissività che alle più alte temperature si avvicina a quella del corpo nero, come mostrato in figura.

 

 

 

 

 

Con le precedenti ipotesi restrittive si ha un’andamento dei due rendimenti come schematizzato nel seguente diagramma che riporta separatamente il rendimento di Carnot (indipendente dal fattore di concentrazione) ed i vari rendimenti di concentrazione parametrizzati appunto con il valore c.

Sull’asse delle ascisse è riportato il valore h_u, che in prima approssimazione può anche essere letto come la sopraelevazione della temperatura del ricevitore rispetto alla temperatura ambiente.

 

 

 

 

Moltiplicando le due componenti si evidenzia il fatto che il rendimento massimo del sistema, per ogni fattore di concentrazione si raggiunge con una temperatura di esercizio del ricevitore circa la metà di quella teoricamente raggiungibile.

 

 

 

 

 

 

 

Riportando questi valori massimi, ed i corrispondenti valori di h_u in funzione del fattore di concentrazione, si hanno gli andamenti riportati nelle seguenti due figure.

Il valore di h_u in corrispondenza del quale si ha il massimo rendimento è ottenuto dall’annullamento della derivata della funzione  = f(h_u):

 

 

 

 

 

 

 

 

 

BILANCIO TERMICO REALE

 

 

Con le ipotesi di un concentratore solare che sfrutti al massimo la radiazione diretta solare, cioè con angolo di incidenza nullo (inseguimento solare su due assi), la potenza termica in ingresso al dispositivo sarà la DNI (Direct Normal Irradiance) in W/m² dove la superficie di riferimento è la superficie di apertura (A) del collettore.

La superficie del ricevitore A_r sarà uguale ad A/C dove C è il rapporto di concentrazione del dispositivo solare.

Non considerando altresì perdite per ombreggiamenti reciproci fra le varie schiere di specchi, né le cosiddette “perdite di estremità”, cioè le perdite che nei collettori lineari sono una conseguenza dei raggi terminali che vanno longitudinalmente oltre la fine del ricevitore, si ha il seguente bilancio termico:

 

A DNI = P _utile + P _ottiche + P _{irraggiamento} + P _{conv / conduz}

 

P _utile è la potenza utile ricavata dal dispositivo = A _th DNI dove _th è il rendimento termico globale del collettore, con riferimento alla potenza in ingresso A DNI.

 

segue  pagina 2 di 6